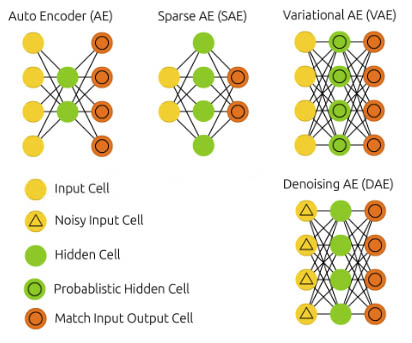
Types of Autoencoders
The ability to compress and rebuild input data without being specifically instructed on which characteristics to extract makes autoencoders a special kind of neural network. There are various categories of autoencoders, each having a marginally different architecture and goal. Here are a few typical autoencoder types:
- Vanilla Autoencoder
- Denoising Autoencoder
- Convolutional Autoencoder
- Variational Autoencoder
- Recurrent Autoencoder
- Sparse Autoencoder
- Contractive Autoencoder
- Fully Connected Autoencoder
Vanilla Autoencoder
The most basic type of autoencoder, which consists of a decoder network that reconstructs the input from the compressed representation after the input has been compressed by an encoder network.
- Purpose: The Vanilla Autoencoder is a straightforward neural network design with the aim of learning to compress input data into a low-dimensional representation and then recover the original input from this representation. This particular autoencoder's objective is to preserve the most crucial aspects of the input data while minimizing the amount of data that is lost during compression.
- Inventor: In 1985, D. H. Ackley and G. E. Hinton made the initial suggestion for the Vanilla Autoencoder.
- Architecture: Encoder and decoder networks make up the two portions of the Vanilla Autoencoder's architecture. The decoder network converts the lower-dimensional representation back to the original input data once the encoder network has converted the input data to it.
- Working: The Vanilla Autoencoder reduces the reconstruction error between the input's original value and the decoder network's output. Usually, a loss function like mean squared error (MSE) or binary cross-entropy (BCE) is used for this.
- Application: Image and video compression, anomaly detection, and dimensionality reduction are just a few of the many uses for vanilla autoencoders.
Denoising Autoencoder
Using corrupted data as training input and clean data as the objective, a denoising autoencoder can be trained to remove noise from input data.
- Purpose: The Denoising Autoencoder is a subclass of autoencoder that learns to filter out noise from input data. A robust representation of the input data that is less sensitive to noise is what this kind of autoencoder aims to learn.
- Inventor: In 2008, P. Vincent, H. Larochelle, Y. Bengio, and P.-A. Manzagol made the initial suggestion for the Denoising Autoencoder.
- Architecture: The Denoising Autoencoder shares the same design as the Vanilla Autoencoder, with the exception that it trains on corrupted input data rather than the original data.
- Working: The Denoising Autoencoder minimizes the reconstruction error between the original input data and the output of the decoder network, given the input of corrupted input data.
- Applications: Denoising Autoencoders have been employed in applications including voice and image denoising.
Convolutional Autoencoder
An autoencoder type created exclusively for picture data, using convolutional layers in the encoder and decoder networks.
- Purpose: A particular kind of autoencoder created especially for image data is the convolutional autoencoder. This kind of autoencoder's objective is to discover a compressed representation of an input image while preserving spatial information.
- Inventor: M. Zeiler and R. Fergus introduced the Convolutional Autoencoder for the first time in 2013.
- Architecture: Convolutional layers are used in both the encoder and decoder networks of the Convolutional Autoencoder, which allows it to extract spatial information from the input image.
- Working: Convolutional autoencoding works by reducing the reconstruction error between the input image's original version and the decoder network's output.
- Applications: Image and video compression, image denoising, and image synthesis are just a few applications where convolutional autoencoders have been put to use.
Variational Autoencoder
A sort of generative model that can produce fresh samples from the learned distribution after learning a latent representation of the input data.
- Purpose: The Variational Autoencoder is a form of autoencoder that may produce new samples from the learned distribution of the input data. This particular autoencoder's objective is to learn a compressed representation of the input data that may be applied to the creation of new samples.
- Inventor: D. Kingma and M. Welling introduced the Variational Autoencoder for the first time in 2014.
- Architecture: The Variational Autoencoder's architecture consists of a decoder network and an encoder network that transfer the input data to a probability distribution in latent space. The VAE, on the other hand, learns a probability distribution over the latent space and has a probabilistic interpretation, unlike other kinds of autoencoders.
- Working: The VAE samples a latent vector from a multivariate Gaussian distribution by encoding the input data into a mean and variance vector. After receiving this latent vector as input, the decoder network creates a new sample using the discovered distribution. The objective is to reduce the divergence between the learned distribution and the prior distribution over the latent space, as well as the reconstruction error between the original input data and the decoder network's output.
- Applications: The uses include image synthesis, data compression, and anomaly detection. Variational Autoencoders have been employed in these fields.
Recurrent Autoencoder
This kind of autoencoder, created especially for sequential data, incorporates recurrent neural networks in the encoder and decoder networks.
- Purpose: For sequential data, such as time series or natural language processing, the Recurrent Autoencoder is a form of the autoencoder. This kind of autoencoder aims to retain the temporal information while learning a compressed version of the input sequence.
- Inventor: K. Cho et al. introduced the Recurrent Autoencoder for the first time in 2014.
- Architecture: Recurrent neural network (RNN) layers like LSTM or GRU make up the encoder and decoder networks that make up the Recurrent Autoencoder's architecture.
- Recurrent neural network (RNN) layers like LSTM or GRU make up the encoder and decoder networks that make up the Recurrent Autoencoder's architecture.
- Working: The Recurrent Autoencoder decodes the input sequence back into the original sequence using the decoder network after encoding it into a fixed-length vector representation. The objective is to reduce the reconstruction error between the decoder network's output and the original input sequence.
- Applications: Recurrent Autoencoders have been put to use in areas like time series prediction, language translation, and speech recognition.
Sparse Autoencoders
An autoencoder that learns a sparse representation of the input data by punishing the activation of hidden units is known as a sparse autoencoder.
- Purpose: The Sparse Autoencoder is a form of autoencoder that enforces sparsity in the learned representation while learning a compressed version of the input data. This kind of autoencoder learns a condensed representation of the input data that captures its key characteristics.
- Inventor: A. Ng et al. made the initial suggestion for the sparse autoencoder in 2011.
- Architecture: The design of the Sparse Autoencoder is identical to that of the Vanilla Autoencoder, but it includes an additional regularization term that promotes sparse activations of the hidden units.
- Working: The Sparse Autoencoder minimizes the reconstruction error between the input data used initially and the output produced by the decoder network while simultaneously punishing the activation of concealed units that do not aid in the reconstruction.
- Applications: Sparse Autoencoders have been applied to features such as feature selection, anomaly detection, and image denoising.
Contractive Autoencoder
An autoencoder type that learns a reliable representation of the input data by punishing the model's susceptibility to minor input perturbations.
- Purpose: The Contractive Autoencoder is a form of autoencoder that enforces robustness to minor input perturbations while learning a compressed representation of the input data. A compact representation that captures the most crucial aspects of the input data and is impervious to minute alterations is what this kind of autoencoder aims to learn.
- Inventor: A. Rifai et al. first put forth the Contractive Autoencoder in 2011.
- Architecture: The Contractive Autoencoder shares the same design as the Vanilla Autoencoder, but adds a regularization term to reduce the hidden units' sensitivity to slight input changes.
- Working: The Contractive Autoencoder minimizes the reconstruction error between the original input data and the decoder network's output while also penalizing the hidden units' sensitivity to minute input changes.
- Application: Contractive Autoencoders have been applied to feature extraction, anomaly detection, and image denoising.
Fully Connected Autoencoder
- Purpose: In order to learn unsupervised material, neural networks with fully connected autoencoders (FCAEs) are used. They are made to train a neural network to encode input data into a lower-dimensional space, learn a compressed representation of the data, and then decode the data back into the original space with the least amount of information loss. Anomaly detection, data visualization, and feature extraction are just a few downstream tasks that can be performed using compressed representation.
- Inventor: The concept of autoencoders was first proposed in the 1980s, and the design has undergone numerous changes over time. In a 1986 publication, Rumelhart, Hinton, and Williams suggested the first fully connected autoencoder.
- Architecture: A fully linked autoencoder is made up of a bottleneck layer in the middle, a decoder network, and an encoder network. The input data is received by the encoder network, which then transfers it to a compressed form in the bottleneck layer. The compressed form is then used by the decoder network to map it back to the original data space. The input and output layers of an encoder and decoder network are normally symmetrical, and the bottleneck layer has fewer neurons than the other layers.
- Working: To reduce the reconstruction error between the input data and the decoder network's output, the fully connected autoencoder is trained.
- For binary input data, this is often accomplished by reducing the binary cross-entropy loss or the mean squared error (MSE) loss between the input and output.
- Backpropagation and gradient descent is used to update the encoder and decoder networks' weights during training. In order to minimize the loss, the weights are updated and the gradients are computed with respect to the loss function.
- Applications: Following training, the bottleneck layer's compressed representation can be applied to a variety of downstream applications. Fully lined autoencoders have been employed in a wide range of applications, including dimensionality reduction, anomaly detection, data denoising, and picture compression. They have also been employed in machine translation and language synthesis jobs in natural language processing.
These are but a few types of the numerous autoencoders that are available. The particular issue and the qualities of the input data determine which autoencoder should be used.
Implementation
Dataset: MNIST
Platform: Colaboratory
By using some of the Autoencoders, let's implement the source code using the keras and visualize the results.
Source code
import numpy as np
import matplotlib.pyplot as plt
from keras.datasets import mnist
from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D, Flatten, Reshape, LSTM, RepeatVector, TimeDistributed
from keras.models import Model
from keras import regularizers
from tensorflow.keras import layers
from tensorflow.keras import backend as K
# Load the MNIST dataset
(x_train, _), (x_test, _) = mnist.load_data()
# Normalize the pixel values to be between 0 and 1
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
# Flatten the images into a 784-dimensional vector for the fully connected autoencoder
x_train_fc = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test_fc = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))
# Define the input shape
input_shape = (28, 28, 1)
# Define the fully connected autoencoder
input_fc = Input(shape=(784,))
encoded_fc = Dense(32, activation='relu')(input_fc)
decoded_fc = Dense(784, activation='sigmoid')(encoded_fc)
autoencoder_fc = Model(input_fc, decoded_fc)
# Define the convolutional autoencoder
input_cnn = Input(shape=input_shape)
x_cnn = Conv2D(16, (3, 3), activation='relu', padding='same')(input_cnn)
x_cnn = MaxPooling2D((2, 2), padding='same')(x_cnn)
x_cnn = Conv2D(8, (3, 3), activation='relu', padding='same')(x_cnn)
x_cnn = MaxPooling2D((2, 2), padding='same')(x_cnn)
x_cnn = Conv2D(8, (3, 3), activation='relu', padding='same')(x_cnn)
encoded_cnn = MaxPooling2D((2, 2), padding='same')(x_cnn)
x_cnn = Conv2D(8, (3, 3), activation='relu', padding='same')(encoded_cnn)
x_cnn = UpSampling2D((2, 2))(x_cnn)
x_cnn = Conv2D(8, (3, 3), activation='relu', padding='same')(x_cnn)
x_cnn = UpSampling2D((2, 2))(x_cnn)
x_cnn = Conv2D(16, (3, 3), activation='relu')(x_cnn)
x_cnn = UpSampling2D((2, 2))(x_cnn)
decoded_cnn = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x_cnn)
autoencoder_cnn = Model(input_cnn, decoded_cnn)
# Define the sparse autoencoder
input_sparse = Input(shape=(784,))
encoded_sparse = Dense(32, activation='relu', activity_regularizer=regularizers.l1(10e-5))(input_sparse)
decoded_sparse = Dense(784, activation='sigmoid')(encoded_sparse)
autoencoder_sparse = Model(input_sparse, decoded_sparse)
# Define the recurrent autoencoder
input_rnn = Input(shape=(28, 28))
encoded_rnn = LSTM(32)(input_rnn)
decoded_rnn = RepeatVector(28)(encoded_rnn)
decoded_rnn = LSTM(32, return_sequences=True)(decoded_rnn)
decoded_rnn = TimeDistributed(Dense(28, activation='sigmoid'))(decoded_rnn)
autoencoder_rnn = Model(input_rnn, decoded_rnn)
# Define the variational autoencoder
input_vae = Input(shape=(784,))
encoded_vae = Dense(256, activation='relu')(input_vae)
z_mean = Dense(2)(encoded_vae)
z_log_var = Dense(2)(encoded_vae)
# Define a sampling function to sample from the learned distribution
def sampling(args):
z_mean, z_log_var = args
epsilon = K.random_normal(shape=(K.shape(z_mean)[0], 2))
return z_mean + K.exp(0.5 * z_log_var) * epsilon
z = layers.Lambda(sampling)([z_mean, z_log_var])
decoded_vae = Dense(784, activation='sigmoid')(z)
autoencoder_vae = Model(input_vae, decoded_vae)
# Compile all the autoencoders
autoencoder_fc.compile(optimizer='adam', loss='binary_crossentropy')
autoencoder_cnn.compile(optimizer='adam', loss='binary_crossentropy')
autoencoder_sparse.compile(optimizer='adam', loss='binary_crossentropy')
autoencoder_rnn.compile(optimizer='adam', loss='binary_crossentropy')
autoencoder_vae.compile(optimizer='adam', loss='binary_crossentropy')
import matplotlib.pyplot as plt
import numpy as np
# Load an example image
x = x_test[0]
# Predict the output using each autoencoder
x_fc_pred = autoencoder_fc.predict(np.expand_dims(x.flatten(), axis=0)).reshape(28, 28)
x_cnn_pred = autoencoder_cnn.predict(np.expand_dims(x, axis=0)).reshape(28, 28)
x_sparse_pred = autoencoder_sparse.predict(np.expand_dims(x.flatten(), axis=0)).reshape(28, 28)
x_rnn_pred = autoencoder_rnn.predict(np.expand_dims(x, axis=0)).reshape(28, 28)
x_vae_pred = autoencoder_vae.predict(np.expand_dims(x.flatten(), axis=0)).reshape(28, 28)
# Plot the original image and the predicted outputs
fig, axs = plt.subplots(1, 6, figsize=(15, 3))
axs[0].imshow(x, cmap='gray')
axs[0].set_title('Original')
axs[1].imshow(x_fc_pred, cmap='gray')
axs[1].set_title('Fully Connected AE')
axs[2].imshow(x_cnn_pred, cmap='gray')
axs[2].set_title('Convolutional AE')
axs[3].imshow(x_sparse_pred, cmap='gray')
axs[3].set_title('Sparse AE')
axs[4].imshow(x_rnn_pred, cmap='gray')
axs[4].set_title('Recurrent AE')
axs[5].imshow(x_vae_pred, cmap='gray')
axs[5].set_title('Variational AE')
plt.show()
- This code implements many autoencoder neural network types, including fully connected autoencoders, convolutional autoencoders, sparse autoencoders, recurrent autoencoders, and variational autoencoders.
- The MNIST dataset is loaded, the pixel values are normalized to be between 0 and 1, and the images are flattened into a 784-dimensional vector for the fully connected autoencoder.
- Then, using the binary cross-entropy loss function and the Adam optimizer, each autoencoder model is defined and assembled.
- Last but not least, the code imports an example image from the test set, forecasts the output using each autoencoder, and shows the original image and the forecasted outputs.
Conclusion
Using Keras, five different kinds of autoencoders have been developed and compiled. These categories include variational autoencoder, fully connected autoencoder, convolutional autoencoder, sparse autoencoder, and recurrent autoencoder.
A fully connected autoencoder learns to compress and then decompress the input data. It is a simple autoencoder with a single hidden layer. A hierarchical representation of the input data is learned by the convolutional autoencoder using convolutional layers, and this representation is subsequently decoded using deconvolutional layers. A regularization term is introduced to a sparse autoencoder, which is identical to a fully connected autoencoder but promotes the network to learn sparse representations. To identify the temporal connections in sequence data, recurrent autoencoder employs recurrent layers.
The variational autoencoder is a probabilistic model that learns to decode input data back into its original form after encoding it as a probability distribution in a latent space.
Each form of the autoencoder is ideal for various sorts of input data and applications, and each has strengths and shortcomings of its own. Examples include the widespread usage of convolutional autoencoders for image data and the suitability of recurrent autoencoders for sequential data, such as time series or natural language data. A compact and understandable representation of the input data can be learned using sparse autoencoders, whereas new data samples are produced using variational autoencoders. In general, autoencoders are an effective tool for unsupervised learning and have a wide range of applications in diverse domains like computer vision, natural language processing, and speech recognition.
References


.png)

